Sortiranje niza - Shellsort

Najveći problem Insertion sort algoritma je potencijalno veliki broj zamena koji se vrši kako bi se svaki elemenat "dovukao" na odgovarajuću poziciju. Jedno od šire poznatih rešenja ovog problema je l959. godine, predložio D. L. Shell, što je postao algoritam poznat kao Shellsort.

Ideja koja stoji iza ovog algoritma je da se sortiranje "razbije" na etape. Prvo se vrši "grubo" sortiranje, a sa svakom sledećom etapom, postaje sve finije i preciznije. Pomoću grubog sortiranja, elementi se dosta brzo prebace na "otprilike" ispravnu poziciju, tako da posle nema puno premeštanja elemenata. Ova optimizacija ima smisla, pošto Insertion sort jako dobro radi sa nizom koji je skoro sređen.

Kako funkcioniše ovo "grubo" sortiranje?

Zamislite da u nizu ne gledamo sve elemente, već recimo, svaki deseti. Tako bismo sortirali samo izabrane elemente, npr. one na pozicijama 1, 11, 21, 31... dok bismo sve ostale ignorisali. Onda bismo uradili to isto, ali na sledećoj poziciji, odnosno, sortirali bismo elemente 2, 12, 22, 32... i tako sve dok ne obavimo sortiranje i elemenata 10, 20, 30, 40...

Šta smo ovime postigli?

Setite se kako funkcioniše Insertion sort - element se "vuče" prema početku niza sve dok ne stigne do svoje tačne pozicije. Za neke elemente će se desiti da mora da se obavi baš velik broj zamena. Ako radimo na "preskok", npr. sa svakim desetim elementom, elementi će doći na pozicije 10 puta brže! Jedini problem je što ta pozicija nije zaista prava pozicija elementa, ali je "tu negde".

Zbog toga onda krećemo u finije sortiranje, npr. svakog trećeg elementa. Pošto su elementi već grubo poređani, neće se dešavati da moramo da "vučemo" puno elemenata od kraja ka početku.

Konačno, poslednja iteracija će biti sa preskokom 1, odnsono klasičan Insertion sort, ali pošto je niz već skoro uređen, ovde će biti izvedene samo sitne korekcije!

Evo i ilustracije koja će vam pomoći da bolje "zamislite" fuunkcionisanje ovog algoritma.

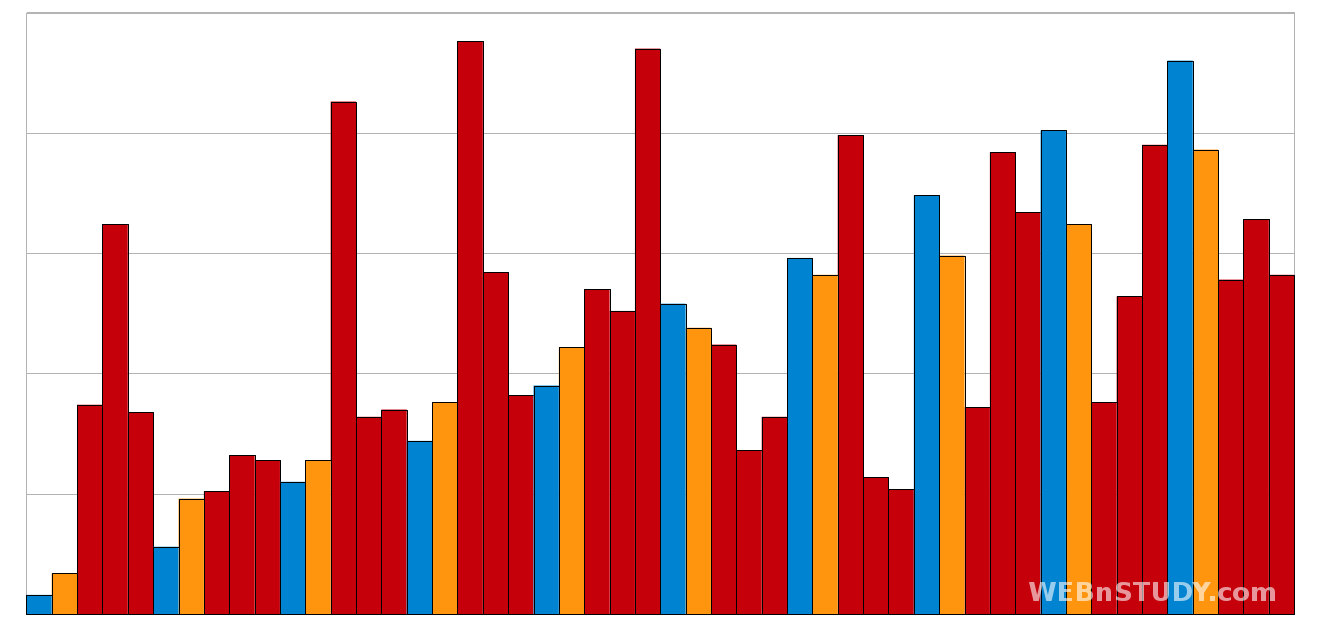
Kako funkcioniše Shellsort algoritam — Ovo je situacija kada smo **tek počeli sortiranje** i kao primer je uzeto da se **sortira svaki peti element**. **Najpre su sortirani plavi elementi** (prvi, šesti, jedanaesti...) i oni su **sortirani međusobno, kao da drugi elementi ne postoje**. Onda se **i dalje sortira sa istim razmakom, samo sa susednim elementima** (narandžasto obojeni elementi - drugi, sedmi, dvanaesti...).

Vidimo da posle prvog, grubog sortiranja, elementi svakako ne budu poređani kako treba, ali su "tu negde". Manji elementi su bliži početku, veći elementi su bliži kraju niza. Kasnije, kada budemo preciznije sortirali, neće biti mnogo komešanja.

Izbor veličine raskoraka

Glavni problem koji se javlja kod ovog algoritma je sa kolikim raskorakom među elementima ćemo raditi u kom prolazu? Drugim rečima, treba izabrati takav niz "preskoka" (tzv. inkrementalnu sekvencu), koji je optimalan. Ako izaberemo previše brojeva, sa malom razlikom u preskocima, "vrtećemo" se previše puta kroz niz. Ako brojevi nisu dobro izabrani, dolazimo u opasnost da neke elemente "gađamo" više puta od drugih.

Ono što bi nam svima (pa i samom tvorcu algoritma) prvo palo na pamet je korišćenje sekvence bazirane na stepenima broja 2. Dakle to bi bio niz preskoka poput ...64, 32, 16, 8, 4, 2, 1, dakle, sortirali bismo prvo elemente na svakoj 64-toj poziciji, pa posle elemente na svakoj 32-goj poziciji i tako dalje. Međutim, ova sekvenca nije baš dobra, pošto se stalno "pogađaju" elementi na rastojanjima koja su deljiva jedna drugima, u nekim situacijama možemo da završimo sa velikim brojem zamena u poslednjoj iteraciji (kada je razmak 1).

Idealan niz raskoraka suštinski nije "dokazan" - uglavnom različiti autori predlažu različite sekvence na osnovu empirijskih podataka, drugim rečima, na osnovu isprobavanja.

Jedna od najpoznatijih i najčešće citiranih sekvenci (pre svega zbog dobrih rezultata i lakoće računanja), dobija se po iterativnoj formuli D. Knutha: h = 3*h + 1, gde krećemo od h=1 i računamo dok ne stignemo do maksimalnog (početnog) raskoraka koji je negde u rangu trećine broja elemenata niza (bitno da bude manje od polovine). Svaki sledeći raskorak u sekvenci dobija se kao celobrojna vrednost prethodnog raskoraka podeljenog sa 3.

Generalno, nije lako matematički dokazati ni efikasnost samog Shellsort algoritma, a kamoli neke određene sekvence. Kao ilustraciju uzmite da je na slučajnom nizu brojeva od 100,000 elemenata, Shellsort i do 600 puta brži od običnog Insertion sorta. Kako se povećava veličina niza, to je sve više efikasniji u odnosu na Insertion sort.

Inače, Shellsort nije stabilan algoritam, što znači da može da se desi da elementi sa istim vrednostima zamenjuju mesta.

Pogledajmo implementaciju u pseudo-kodu.

Shellsort algoritam

Treba da znamo da je ovde izvedena jedna optimizacija. Zamislite na trenutak da je raskorak H=10. Umesto da vrtimo H zasebnih ciklusa (tačnije onoliko ciklusa koliki nam je raskorak - prvo za 1,11,21... pa onda za 2,12,22...) sve obavljamo u jednom ciklusu!

Dakle umesto da prolazimo kroz elemente sa preskocima, mi prolazimo kroz sve elemente, ali ih sortiramo samo sa njihovim elementima "rođacima" - kroz preskoke.

Tako na primer, kada stignemo do 21. elementa, njega sortiramo sa elementima 11 i 1. Međutim, onda ne skačemo na element 31, već na 22, koji sortiramo sa "njegovim" elementima 12 i 2.

Evo i samog algoritma...


  
  global {a;} n = 200; a = array(n); for (i = 1..n) { a[i] = trunc(rand()*1000); } write("Elementi niza:"); ispisNiza(n);
  
  h = 1;
  while(h <= n div 3) {
    h = 3*h + 1;
  }
  while (h>1) {
    h = h div 3;
    for (i=h+1..n) {
      x = a[i];
      j = i-h;
      while( radi(j,x) ) {
        a[j+h] = a[j];
        j = j-h;
      }
      a[j+h] = x;
    }
  }
    
  function radi(j,x) {
      if (j >= 1) {
        if (x < a[j]) {
          return (true);
        }
      }
      return (false);
  }
  
  write(" "); write("Sortiran niz:"); ispisNiza(n); provera(n);
  function ispisNiza(n) { t = ""; for (i = 1..n) { t += a[i] + " ";} write(t); }
  function provera(n) {r = true; for (i = 2..n) { r = r and a[i-1]<=a[i];} if(r){write("Niz je neopadajuci");}else{write("Niz NIJE sortiran");}}
  
  Na početku moramo da odredimo raskorak H, zavisno od veličine niza. Počinjemo od 1...
  ...i sve dok je H manje od trećine broja elemenata niza...
  ...računamo veći raskorak po formuli. Ovako dobijeno H će biti veći od trećine, ali to ćemo srediti kad krenemo u sortiranje.
  Sortiranje se vrši sve dok H ne stigne do 1. To je poslednja iteracija, i to je onda najfinije sortiranje -  praktično Insertion sort.
  Svaki sledeći H se dobija kao trećina prethodnog (celobrojna). Pošto smo malo preterali kad smo ga računali, već na početku ciklusa ga delimo sa 3.
  Idemo od početka prema kraju niza, s tim što preskačemo prvih H elemenata (preskačemo elemente prvog raskoraka).
  Taj I-ti element će biti elemenat koji vučemo naniže do njegove pozicije. Zato ga pamtimo u X.
  Brojač J prolazi kroz sve elemente ispred pozicije I, ali na H-tim raskoracima - zato nije i-1 nego i-h.
  Ovde se vrši provera dokle treba da vučemo I-ti element. Sve dok J može da se smanjuje u koracima od po H i dok je X manji od elemenata koje sortiramo...
  ...pomeramo elemente naviše (u koracima od po H, naravno)...
  ...i opet smanjujemo J za H.
  Kad smo izašli iz ciklusa, znamo da smo našli poziciju na koju treba prebaciti I-ti element (zapamćen kao X) i to i radimo.
    Moramo imati korekciju pozicije (J+H), zato što smo u ciklusu "preterali" - kada je konačno trebalo da se izađe iz ciklusa,
    smanjili smo J za jedno H previše.
  
  Ovo je prosto funkcija koja sprovodi u delo našu proveru kompleksnog uslova.
  Ako je J ispravan (nije skliznuo ispod 1 zbog stalnog oduzimanja vrednosti H)...
  ...i ako je X i dalje manje od J-tog elementa, vratićemo vrednost TRUE, što znači da se WHILE ciklus nastavlja.

Kako sve to funkcioniše, možete pogledati i u grafičkom primeru.

Shellsort grafički primer

Ne zaboravite, zbog stalnog iscrtavanja, grafička reprezentacija funkcionisanja algoritma ne odslikava njegovu realnu brzinu.


  
  global {
    a,n,s,vis, bru,brz;
  }
  n = 50;
  a = array(n);
  for (i = 1..n) {
    a[i] = trunc(rand()*_HEIGHT/2) + 10;
  }
  color("#000");
  
  vis = _HEIGHT - _HEIGHT / 4;
  s = _WIDTH / n;
  bru=0;
  brz=0;

  crtaj();
  h = 1;
  while(h <= n div 3) {
    h = 3*h + 1;
  }

  while (h>1) {
    h = h div 3;
    write("Raskorak: " + h);
    for (i=h+1..n) {
        x = a[i];
        j = i-h;
        while( radi(j,x,i) ) {
          a[j+h] = a[j];
          brz++;
          j = j-h;
        }
        a[j+h] = x;
        crtaj();
    }
  }
    
    function radi(j,x,i) {
      if (j >= 1) {
        poredi(i,j);
        if (x < a[j]) {
          return (true);
        }
      }
      return (false);
    }

  write(n + " elemenata");
  write(bru + " upoređivanja");
  write(brz + " zamena");
  
  function poredi(i,j) {
    bru++;
    fill("#ffb"); rect((i-1)*s, vis-a[i], s,a[i]); fill("#fff"); rect((j-1)*s, vis-a[j], s,a[j]); graphic();
    fill("#aaa"); rect((i-1)*s, vis-a[i], s,a[i]); rect((j-1)*s, vis-a[j], s,a[j]); graphic();
  }
  function crtaj() {
    cls("#444"); fill("#aaa"); for (i = 1..n) { rect((i-1)*s, vis-a[i], s,a[i]); } graphic();
  }

R. Sedgewick, K. Wayne (2011): Algorithms, Boston: Pearson
G. Heineman, G. Pollice, S. Selkow (2010): Algorithms in a Nutshell, Sebastopol: O’Reilly Media
S. Harris, J. Ross (2006): Beginning Algorithms, Indianapolis: Wiley
T. Cormen, C. Leiserson, R. Rivest, C. Stein (2009): Introduction to Algorithms, Cambridge: MIT Press
N. Wirth (1985): Algorithms and Data Structures, New Jersey: Prentice Hall

Svi elementi sajta Web'n'Study, osim onih za koje je navedeno da su u javnom vlasništvu, vlasništvo su autora i ne smeju se koristiti, u celosti ili delimično bez pismenog odobrenja autora. To uključuje tekstove, slike, ilustracije, animacije, prateći grafički materijal i programski kod.

Ovaj sajt koristi tehnologiju kolačića (cookies). Detaljnije o tome možete pročitati u tekstu o našoj politici privatnosti.